Non-associative algebra

This article is about a particular non-associative structure known as a non-associative algebra. See also the article about non-associativity in general.

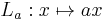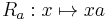A non-associative algebra^[1] (or distributive algebra) over a field (or a ring) K is a K-vector space (or more generally a module^[2]) A equipped with a K-bilinear map A × A → A. There are left and right multiplication maps and . The enveloping algebra of A is the subalgebra of all K-endomorphisms of A generated by the multiplication maps.

An algebra is unital or unitary if it has a unit or identity element I with Ix = x = xI for all x in the algebra.

Examples

The best-known kinds of non-associative algebras are those that are nearly associative—that is, in which some simple equation constrains the differences between different ways of associating multiplication of elements. These include:

• Lie algebras that are anticommutative , which require xx = 0 and the Jacobi identity (xy)z + (yz)x + (zx)y = 0. For these algebras the product is called the Lie bracket and is conventionally written [x,y] instead of xy. Examples include:
  • Euclidean space R³ with multiplication given by the vector cross product (with K the field R of real numbers)
  • Algebras of vector fields on a differentiable manifold (if K is R or the complex numbers C) or an algebraic variety (for general K);
  • Every associative algebra gives rise to a Lie algebra by using the commutator as Lie bracket. In fact every Lie algebra can either be constructed this way, or is a subalgebra of a Lie algebra so constructed.

• Jordan algebras which are commutative and satisfy the Jordan property (xy)x² = x(yx²) and also xy = yx
  • every associative algebra over a field of characteristic other than 2 gives rise to a Jordan algebra by defining a new multiplication x*y = (1/2)(xy + yx). In contrast to the Lie algebra case, not every Jordan algebra can be constructed this way. Those that can are called special.

• Alternative algebras, which require that (xx)y = x(xy) and (yx)x = y(xx). The most important examples are the octonions (an algebra over the reals), and generalizations of the octonions over other fields. (Obviously all associative algebras are alternative.) Up to isomorphism the only finite-dimensional real alternative, division algebras (see below) are the reals, complexes, quaternions and octonions.

• Power-associative algebras, which require that x^mxⁿ = x^m+n, where m ≥ 1 and n ≥ 1. (Here we formally define xⁿ recursively as x(xⁿ⁻¹).) Examples include all associative algebras, all alternative algebras, and the sedenions.

• The hyperbolic quaternion algebra over R, which was an experimental algebra before the adoption of Minkowski space for special relativity.

These properties are related by 1) associative implies alternative implies power associative; 2) commutative and associative implies Jordan implies power associative. None of the converse implications hold.

More classes of algebras:

• Graded algebras. These include most of the algebras of interest to multilinear algebra, such as the tensor algebra, symmetric algebra, and exterior algebra over a given vector space. Graded algebras can be generalized to filtered algebras.

• Division algebras, in which multiplicative inverses exist or division can be carried out. The finite-dimensional alternative division algebras over the field of real numbers can be classified nicely. They are the real numbers (dimension 1), the complex numbers (dimension 2), the quaternions (dimension 4), and the octonions (dimension 8).

• Quadratic algebras, which require that xx = re + sx, for some elements r and s in the ground field, and e a unit for the algebra. Examples include all finite-dimensional alternative algebras, and the algebra of real 2-by-2 matrices. Up to isomorphism the only alternative, quadratic real algebras without divisors of zero are the reals, complexes, quaternions, and octonions.

• The Cayley–Dickson algebras (where K is R), which begin with:
  • C (a commutative and associative algebra);
  • the quaternions H (an associative algebra);
  • the octonions (an alternative algebra);
  • the sedenions (a power-associative algebra, like all of the Cayley-Dickson algebras).

• The Poisson algebras are considered in geometric quantization. They carry two multiplications, turning them into commutative algebras and Lie algebras in different ways.

• Genetic algebras are non-associative algebras used in mathematical genetics.

References